sebelum itu, pastikan anda sudah mengisntal aplikasi Matlab, misal : Matlab R2008a, jika belum memilikinya, sebaiknya kalian mendownloadnya terlebih dahulu dari web penyedia aplikasi tersebut, saya mohon maaf tidak menyediakan link downloadnya.
Baiklah, jika kalian sudah memilikinya, pertama-tama buka dulu aplikasi tersebut, akan tampak seperti dibawah ini :
Misalnya kalian ingin mendapatkan jawaban dari soal laplace berikut ini :
L { 1/64 t ( sin 2t – 2t cos 2t) }
Sebelum memulai menulisnya di matlab, pertama-tama kalian harus menulis "syms t" (untuk soal dengan fungsi t), maksudnya adalah agar aplikasi tersebut membaca fungsi t sebagai system dalam perumusan.
kemudian untuk menulisnya di matlab adalah seperti berikut :
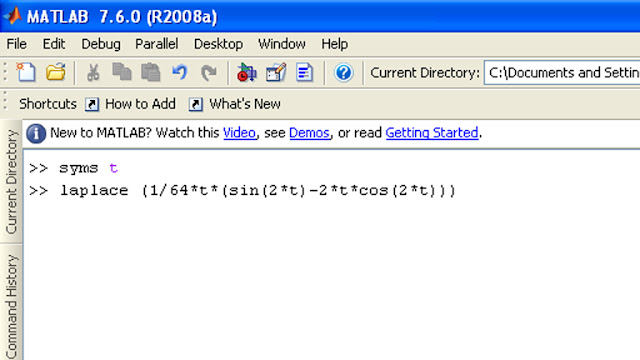
Pertama-tama adalah menuliskan "laplace" kemudian baru memasukkan soal tadi yang hendak kita selesaikan. Dalam matlab, perkalian ditandakan dengan * (bintang), pembagian ditandakan dengan / (se-per), hampir sama seperti aplikasi-aplikasi teknik pada umumnya. Dalam penulisan soal pada matlab, hal yang perlu sangat diperhatikan adalah tanda kurung (.....), jumlah tanda kurung buka yang terpakai harus sama dengan jumlah tanda kurung tutup, jika tidak sama, yang terjadi akan seperti ini (dalam kasus soal yang tadi) :
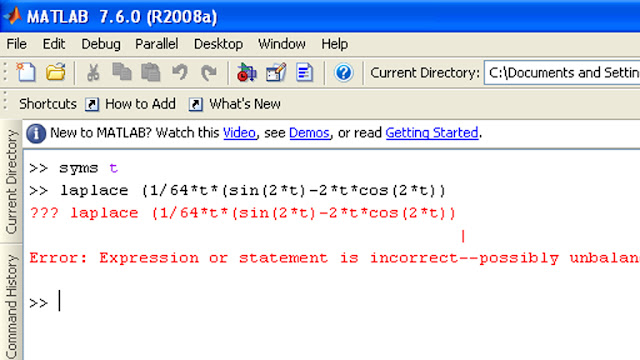
untuk itu tanda kurung perlu sangat diperhatikan, selain mengenai hal tadi, untuk kasus soal yang lebih rumit lagi (kompleks), tanda kurung juga memastikan mana yang lebih dulu diproses oleh sistem, salah memberi tanda kurung mengenai data yang harusnya lebih dahulu diproses, akan dipastikan juga jawaban yang akan diberikan nanti salah. Misalnya seperti soal berikut ini (syms s, karena s sebagai fungsi dalam perumusan) :
L-1 { 3(s2-1)2 +
4s-18 + (s+1) (2 - s1/2)
}
2s5 9-s2 s5/2
Baiklah kembali ke soal sebelumnya, maka akan didapat jawaban seperti berikut :
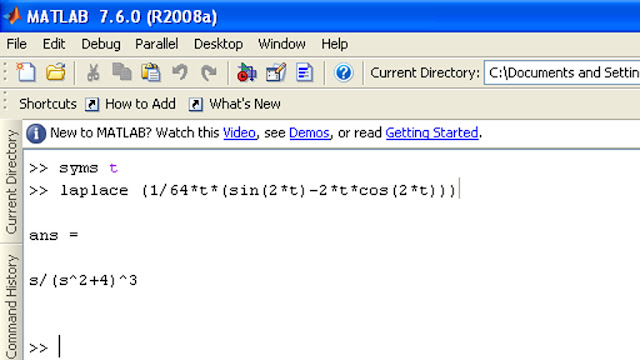
Jika hendak mendapatkan jawaban yang lebih baik lagi, kalian tinggal mengetikkan "pretty (ans)" maka jawaban seperti diatas akan ditampilkan lebih baik lagi. Seperti gambar di bawah ini :

Jawaban yang ditampilkan lebih baik bukan? Baiklah itu merupakan penyelesaian oleh aplikasi, untuk memastikan apakah benar, kalian bisa mengerjakan soal tadi, saya mohon maaf karena jawaban tadi yang akan saya tampilkan berformat *jpg, sebelumnya saya tulis di Ms.Word, kemudian diedit dengan aplikasi AP4, karena sulit dan lama jika ditulis disini (salah satu kelemahan blog G), baiklah berikut jawabannya :
Nah, jawabannya sama kan? itu tandanya soal yang tadi kita tulis di matlab benar, baiklah berikut soal-soal yang bisa kalian coba di matlab, jawaban saya berikan di bawah soal, berikut soal-soalnya :
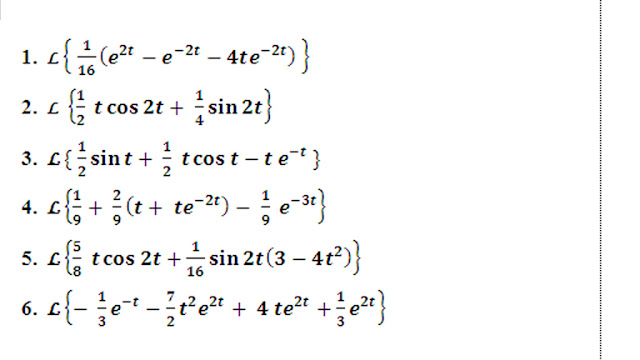
Jawabannya :
1. >>
laplace (1/16*(exp(2*t)-exp(-2*t)-4*t*exp(-2*t)))
ans
=
1/(s-2)/(s+2)^2
>>
pretty (ans)
1
----------------
2
(s
- 2) (s + 2)
2. >> laplace (1/2*t*cos(2*t)+ 1/4*sin(2*t))
ans =
s^2/(s^2+4)^2
>> pretty (ans)
2
s
---------
2 2
(s + 4)
3. >> laplace
(1/2*sin(t)+1/2*t*cos(t)-t*exp(-t))
ans =
(-s^2+2*s^3-1)/(s^2+1)^2/(1+s)^2
>> pretty (ans)
2 3
-s + 2 s
- 1
------------------
2 2
2
(s + 1)
(1 + s)
4. >> laplace (1/9 + 2/9*(t + t*exp(-2*t))-1/9*exp(-3*t))
ans =
1/9*(7*s^3+32*s^2+44*s+24)/s^2/(s+2)^2/(s+3)
>> pretty (ans)
3 2
7 s + 32 s + 44 s + 24
1/9 ------------------------
2 2
s (s + 2) (s + 3)
5. >> laplace (5/8*t*cos(2*t)+1/16*sin(2*t)*(3-4*t^2))
ans =
s^4/(s^2+4)^3
>> pretty (ans)
4
s
---------
2 3
(s + 4)
6. >> laplace (-1/3*exp(-t)-7/2*t^2*exp(2*t)+4*t*exp(2*t)+1/3*exp(2*t))
ans =
(-11-15*s+5*s^2)/(1+s)/(-2+s)^3
>> pretty (ans)
2
-11 - 15 s + 5 s
-----------------
3
(1 + s) (-2 + s)
Baiklah demikianlah cara menggunakan matlab untuk penyelesaian soal matematikan laplace, jika ada kesalahan mohon komentarnya. Terima kasih sudah berkunjung.
Baiklah demikianlah cara menggunakan matlab untuk penyelesaian soal matematikan laplace, jika ada kesalahan mohon komentarnya. Terima kasih sudah berkunjung.






























